When a signal crosses a wire between two sites, representing a message between objects as introduced here, it must identify objects at the destination site. A name space in some guise must be agreed upon by sender and receiver. We consider two plans here for this name space: A link protocol may establish short names for capabilities as a compression technique where the short names are compressed forms of a long global name. The second scheme above refers to those systems where new short link names are established with no corresponding global name.

These notes speak of physical wires between nodes whereas most application distribution these days presumes an available switched network such as Internet. This is partly because I am still on the lookout for a better architecture for such networks. Thus I hesitate to factor the problem in the conventional way.

three site hand-off

First we must consider the three site hand-off issue which arises early in the planning for use of such systems, for this issue impacts the choice of name space plan. 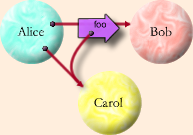This canonical picture is often used to clarify the capability discipline that must be maintained for distributed capabilities. We are concerned here about when A, B and C are each at different sites respectively called Sa, Sb and Sc. We assume initially that there are two wires: We may view the fat arrow in the picture as a signal traveling on the wire from Sa to Sb. When B gets the message it will contain a real reference to a newly created forwarder Cf for C. If B addresses a message via Cf, it must necessarily be routed along available wires: via A and the forwarder in Sa via which A accesses C. Such schemes work correctly with no special three site code. It would be strategic, however, to enable a wire between B and C to carry such messages. Such would often be faster especially if Sa or its wires become unavailable.

Application design naturally limits the sites at which its components arise. We will impose another condition on our protocols: The security of an application will rely only on the correctness of the platforms (including communications protocols) at the sites it chooses to run on. Early versions of Sun’s Java’s RMI failed to meet this condition.

To this end: Nothing at site B should be able to access C until A at Sa sends the depicted message. Furthermore this must not depend on the correctness of the system code at Sb. More succinctly: A site holds no capabilities beyond those legitimately held by its guest objects, or recent guests. An application distributed between Sa and Sc is not vulnerable to a corrupted site Sb unless it explicitly decides to trust Sb, and then only with those references that it sends there.

Three Site Hand-off with a Global Name Space

Perhaps the first idea is to use a sufficiently large random name that they may not be guessed. This requires secrecy on the wires so that untrusted sites will be unable, by wire tapping, to reference objects that they should not be able to reference. Public keys are ideal in this respect except for the cost of processing them. Public keys are, however the obvious choice for the necessary secure identification of sites. The fat arrow must carry a secure site identification as well as the secret object name. Electric Community’s Pluribus protocol (= VatTP + CapTP) does just this. Program logic is included.

Three Site Hand-off with Local Name Spaces

At first glance this seems more complex, for established objects with established names must acquire new names as they become know on new wires. While strong authentication is still required, this plan does not otherwise require secrecy.

Enabling this communication over a wire between Sb and Sc requires establishing a name for C in the space for that wire. The following scheme provides that name but only in the situations permitted by capability discipline.

Suppose that all wire traffic is strongly authenticated with a shared secret and a hash. Diffie-Hellman provides a convenient shared secret and the cost is born only when the wire is installed or a system booted.

When B’s forwarder at Sa builds the signal depicted in the diagram, it recognizes that the reference to C is a remote reference (via a forwarder). In the signal to Sb, Sa includes instructions to Sc, authenticated by the secret shared by Sa and Sc, directing Sc to honor a request by Sb (identified by Sb’s public DH key), for access to C via the wire over which Sb may share with Sc. This indirect message will be delivered to Sc before any message is sent via the transmitted capability.

It may seem strange to send these instructions from Sa to Sc via Sb but this overcomes various combinations of periods of unavailability such as when Sa is unavailable when b wishes to first use the transmitted capability, or when Sc is unavailable when the depicted signal is sent.

One advantage is that names need be only large enough to distinguish the objects involved with the traffic on a given wire. When local garbage collection observes no further references to a forwarder, the forwarder and name it uses to identify its master may be retired. When A has launched its message to B precautions must be taken to preserve the forwarder to C at Sa until the indirect instructions have been acted upon. Otherwise those instructions may refer to a reused name between Sa and Sb. This can be done by preserving a reference at Sa to C until notification from Sb that C has been named at Sb.

This scheme is reminiscent of the Needham-Schroeder scheme used in Kerberos.

Alternate local space hand-off

In the Client Utility Architecture Sa sends the introduction directly to Sc. This is more direct and probably less work if the transmitted capability is actually used. Sc gets involved in this case even if Sb never invokes the capability.

Ramifications

There are these bothersome ramifications to the local name scheme. In the three node handoff described above Sc gets an authentic message within an authentic message. The outer authentication means that the message is from Sb and this indicates to Sc that Sb came somehow to hold the inner message. The inner message is authentically from Sa, even if indirectly. Sc has a trust relationship with Sa and is thus willing to act on this to duplicate the local capability so as to make that capability wieldable upon signals from Sb.

This convinces me that the inner message is a bearer instrument issued by the holder of the real capability and usable be nearly anyone who knows the bits. If a corrupted node is outside the set that is trusted by the application learns the bits of the instrument, it may present them and thus wield the capability. Protecting against this threat seems to require keeping the bits of the instrument secret. I think we are back to the secret swiss number.

Synthesis

I conclude that the two schemes introduced at the beginning can each be considered as optimizations of the other. I don’t see a strong advantage of either over the other. Perhaps in the second scheme one can defer the expense of generating a swiss number until more than two nodes must hold a capability.