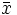Clifford algebras were invented to understand rigid transformations on their base space V.
To explore the zero divisors of C we consider the action on C of multiplying on the left by an element x of C.
In particular consider the action of multiplying by an element of {x| m(x)=1}
where “m(x)” = |x|<sup>2</sup> = &lt;<img src=xbar.png>x> = (mag2 x)
= (sum of squares of scalar coefficients in basis expansion of x) .
λx.m(x) = m is not one of the functions normally of significance in Clifford algebras but it is a coordinate free function.
Some of these formulae fail if V’s quadratic form is not positive definite.
<p>m(xy) = m(x)m(y) is true for <a href=../DivAlg.html>octonions but not for sedenions</a>.
Octonions are a divisions algebra and sedenions are not even though most sedenions have inverses.
m(xy) = m(x)m(y) is true for Cl(n, 0) only if 0≤n<3.
<p><b>Definitions</b> for this page
<p><b>C</b> = Cl(4, 0),
<br><b>V</b> is the 4D space within C that generates C,
<br><b>B<sub>V</sub></b> = {γ<sub>0</sub>, γ<sub>1</sub>, γ<sub>2</sub>, γ<sub>3</sub>} is an orthonormal basis for V,
<br><b>t</b> = γ<sub>0</sub>γ<sub>1</sub>γ<sub>2</sub>γ<sub>3</sub>,
<br>For set x, <b>P(x)</b> is the power set of x, sometimes written 2<sup>x</sup>.
It is the set of subsets of x.
<br>If x ⊆ C and x is finite then <b>Π(x)</b> is the product of the elements of x. &Pi;(∅) = 1. Π(B<sub>V</sub>) = t.
(&Pi; is ambiguous due to lack of commutativity but I use it where the only ambiguity is the sign and where sign doesn't matter.)
<br>If x ⊆ C then <b>−x</b> = {−z | z ∊ x}.
<br>B<sub>C</sub> = {Π(x) | x⊆B<sub>V</sub>} is a basis for C.
<p>The code below reveals that the set B = {a(t+1) | a ∊ C} is an 8 dimensional subspace of left zero divisors which is spanned by a set Q of 8 independent Clifford numbers.
Q = {1+γ<sub>0123</sub>,  γ<sub>0</sub>+γ<sub>123</sub>,
γ<sub>1</sub>−γ<sub>023</sub>,  γ<sub>01</sub>−γ<sub>23</sub>,
γ<sub>2</sub>+γ<sub>013</sub>,  γ<sub>02</sub>+γ<sub>13</sub>,
γ<sub>12</sub>−γ<sub>03</sub>,  γ<sub>012</sub>−γ<sub>3</sub>}.
<p>The code works as follows:
Q = {x(t+1)|x ∊ B<sub>C</sub>}.
Q spans B.
<p>B is closed under multiplication.
An example of aa=0: (γ<sub>0</sub>+γ<sub>123</sub>)(γ<sub>0</sub>+γ<sub>123</sub>) = 0.
<hr>The code below uses definitions from <a href=synTools1.html>here</a>.
<pre>
; generate set of subsets where set is a list:
(define (P a) (if (null? a) '(()) (let ((c (car a))) (let L ((x (P (cdr a))))
    (if (null? x) '() (cons (car x) (cons (cons c (car x)) (L (cdr x)))))))))

; multi operand multiply:
(define (lm x)(if (null? x) C1 (C* (car x) (lm (cdr x)))))

; generate all subsets of basis for V then generate basis for C.
(define CB (map lm (map reverse (P (reverse basis)))))

; numlist turns a number tree into a list of numbers.
; below a must be a number tree and b a number list. Returns a number list.
(define (numlist a) (let nl ((a a)(b '())) (if (number? a) (cons a b)
    (nl (car a) (nl (cdr a) b)))))

; observe generation of basis for C suitable for rank software.
; (map numlist (map lm (map reverse (P basis)))) ; => twist permutation.

(define Q (map numlist
  (let ((T (C+ C1 (C* (C* g0 g1) (C* g2 g3)))))
    (map (lambda (p) (C* p T)) (map lm (map reverse (P basis)))))))
<hr>
Q => (
(1  0 0  0  0 0  0 0 0  0 0  0  0 0  0 1)
(0  0 0  0  0 0  0 1 1  0 0  0  0 0  0 0)
(0  0 0  0  1 0  0 0 0  0 0 -1  0 0  0 0)
(0  0 0 -1  0 0  0 0 0  0 0  0  1 0  0 0)
(0  0 1  0  0 0  0 0 0  0 0  0  0 1  0 0)
(0  0 0  0  0 1  0 0 0  0 1  0  0 0  0 0)
(0  0 0  0  0 0  1 0 0 -1 0  0  0 0  0 0)
(0 -1 0  0  0 0  0 0 0  0 0  0  0 0  1 0)
(0  1 0  0  0 0  0 0 0  0 0  0  0 0 -1 0)
(0  0 0  0  0 0 -1 0 0  1 0  0  0 0  0 0)
(0  0 0  0  0 1  0 0 0  0 1  0  0 0  0 0)
(0  0 1  0  0 0  0 0 0  0 0  0  0 1  0 0)
(0  0 0  1  0 0  0 0 0  0 0  0 -1 0  0 0)
(0  0 0  0 -1 0  0 0 0  0 0  1  0 0  0 0)
(0  0 0  0  0 0  0 1 1  0 0  0  0 0  0 0)
(1  0 0  0  0 0  0 0 0  0 0  0  0 0  0 1))
which is of rank 8.
The first 8 are independent and for i = 0 thru 7
(15-i)th vector is same or negative of ith vector.
</pre><hr>
Now include the definitions of <a href=../../../code/Scheme/transpose.html>trnxx and transpose </a> and <a href=../../Field/index.html>matpak, ops and inv</a> and <a href=../../Field/Rank.html>Rank</a>.

<pre>

(define (treestr x) (let ld ((x x)) (if (and (pair? x)(null? (cdr x))) (car x)
  (ld (let z ((x x)) (if (and (pair? x)(pair? (cdr x)))
    (cons (cons (car x)(cadr x)) (z (cddr x))) '()))))))

(define trn transpose)
; The following computes the smallest subset of Q that spans what Q does.
(define Q (map treestr (trn (Rank (trn Q)))))
; Q is the computed set referred to above and (Sr Q) generates random elements form B.
</pre>
<a href=ZD3.html>Here</a> we automate this so we can perform this process on other discovered zero divisors.