This program can be easily extended to compute moments of the intersection. Since the intersection of polygons may not be a polygon one cannot do the obvious thing of yielding a polygon as the intersection of two. One could introduce a polygon set abstraction and build the closed intersection operator for those. That, however, is more work than is necessary for the area.
An ANSI C version at github
It may seem strange to use a type such as hp in the program rather than double. It is necessary not for precision of the answer but to avoid common degenerate cases where points are nearly collinear. To avoid multitudinous degenerate cases, each of which is trivial but which are collectively overwhelming, I arrange to entirely avoid collinearity. The values of fudge and c&1 contrive to jiggle the points to avoid a vertex of one polygon lying on an edge of the other. The value of gamut is chosen to avoid overflow in routine area yet minimize the effect of the noise we add to the vertex coordinates. It has to do with there being about 232 values of an int. There must be no rounding of hp values. An untested assertion is thus that area should never return 0. If the signs of routine area were ever wrong then it would probably lead to intersections being missed and in turn gross errors in the output.
There are a few tests at the end that can be worked by hand. This intersects two regular triangles in many orientations to form a regular hexagon, and computes that area.
| ∫ | y dx |
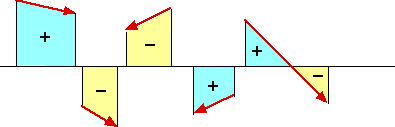
 The integral expression can be applied when the integral is taken around a closed curve, including negative dx’s.
We have thus reduced an integral over the interior of a polygon to an integral over its boundary.
The area is the unordered sum of a function of the oriented sides of the polygon.
It is necessary for the logic of the program that this sum need not be ordered.
This calculation works for collections of polygons as well, yielding the sum of the areas.
The integral expression can be applied when the integral is taken around a closed curve, including negative dx’s.
We have thus reduced an integral over the interior of a polygon to an integral over its boundary.
The area is the unordered sum of a function of the oriented sides of the polygon.
It is necessary for the logic of the program that this sum need not be ordered.
This calculation works for collections of polygons as well, yielding the sum of the areas.
This is the same sort of math upon which the planimeter is based.
Consider the integral below along the boundary of one simple polygon:
| ∫ | w y dx |
Here we discuss the determination of the topology of the sides of the polygons. Here is a high level view of the algorithm with references to the code. See this for some fragmentary theory.
groping for polyhedra
Further out
A 3D version.
This sounds like a general system.
an application