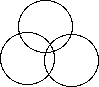
As before Cx means that x is a connected open point set.
ϕ₂ = ∃a∃b∃c∃d(Ca∧Cb∧Cc∧Cd∧(every three intersect) ∧ a∩b∩c∩d = ∅)
ϕ₂ is true in S(2) but not S(1).

In S(n) but not in S(n−1) there are n+2 connected open sets with no common element but any n+1 of which intersect. This is not equivalent to the Lebesgue Covering Dimension.

Here we see

The Lebesgue covering dimension of a topological space is defined to be the maximum value of n, such that any open cover has a refinement with no point included in more than n+1 elements.

ϕ_n ↔ ∀x[CV(x) → ∃z(z ⊆ x ∧ CV(z) ∧ ∀w(w∊X →
(∃y₁ ∃y₂ ... ∃y_n+2( w∊y₁∧y₁∊z ∧ w∊y₂∧y₂∊z ... ∧ w∊y_n+2∧y_n+2∊z
→ (y₁ = y₂ ∨ y₁ = y₃ ∨ ... y₁ = y_n+2 ∨ y₂ = y₃ ∨ ... y₂ = y_n+2 ∨ ... y_n+1 = y_n+2)))))]

ϕ_n is true in ℝ^m iff n ≥ m. This can be understood intuitively as follows:
In A 1D covering, open sets overlap by pairs to avoid leaving gaps. In 2D a cover must be triply redundant some places in order to cover all:

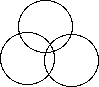
An open cover of a space is merely a set of open sets whose union is the space. The dimensionality definition requires a property of all covers, especially of the covers consisting of small open sets. And then it can require it of only sub covers of those open sets, for a cover with more open sets added is still a cover. You can always remove superfluous members of a cover until you get to the point where no point belongs to more than n+1 members of the cover, in an n dimensional space. This definition constrains every non-empty open set to be n dimensional. The dimension of a hybrid set, such as 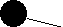is 2. It is easy to require that every non-empty open set in the space be of the same dimension which would rule out this case.

My definition assigns a dimension of 2 to some curves that can be drawn on a plane. The Lebesgue Covering Dimension of these would be 1. Requiring each non-empty open set to be the same dimension in my sense is easy too. I don't know if it is then equivalent to Lebesgue’s dimension.