fileVal (or here) is the code required for the repository logic. The first version is provides some extra security but depends on optional features that some Schemes lack. The second version works on more Schemes and but relies on deprecated language features. (See this for Racket.) Why two fileVals. I copy one of these two definitions of fileVal immediately upon launching the interactive Scheme interpreter.

Do

I prefer and use these functions to the official Scheme syntactic sugar.

(((fileVal "Do") 'Do) 6 (lambda (j) (write (+ j 2)))) ; => 765432
(((fileVal "Do") 'DoL) 5 (lambda (j) (* j 2))) ; => (0 2 4 6 8)
(((fileVal "Do") 'DoV) 4 (lambda (j) (+ j 4))) ; => #(4 5 6 7)
(((fileVal "Do") 'DoF) 7 cons 'end) ; => (0 1 2 3 4 5 6 . end) as in OCaml fold

More info

Equal

An equivalence test for potentially infinite Scheme structures. More info

Seal

Seal creates sealer-unsealer pairs as conceived by James H. Morris: “Protection in Programming Languages”, CACM, 16(1):15-21, 1973. This is my Scheme version of Stiegler’s E version of Morris’ primitive. It supports fairly efficient synergy which I had thought impossible in Scheme. “((fileVal "Seal"))” yields a matched pair: (sealer . unsealer).

(let* ((p ((fileVal "Seal"))) (seal (car p)) (unseal (cdr p))
  (b2 (seal 42)) (b3 (seal 43))) (cons (unseal b2) (unseal b3)))

yields (42 . 43).

(let* ((S (fileVal "Seal")) (b ((car (S)) 42))) ((cdr (S)) b))

yields #f; the unsealer must come from the same pair as the sealer.
The module ‘HSet’ below uses Seal to abstract its implementation.
This code was invented by Mark Stiegler.

RC4

A source of quality pseudo random generators based on the RC4 crypto algorithm. ((fileVal "RC4") seed-string) returns a mutable object whose initial state is determined by the string argument. The state is the abstracted RC4 state.

(let ((g (((fileVal "RC4") "Seed stuff") 'nb))) (list (g 4) (g 3) (g 2)))

yields (3453575773 3264371 6246). (g n) yields integers uniformly distributed in [0, 2⁸ⁿ).

(let ((g (((fileVal "RC4") "Seed stuff") 'sb))) (list (g) (g) (g)))

yields (205 217 98), integers uniformly distributed in [0, 2⁸). These successive values are the eight bit bytes of the RC4 key-stream.

((((fileVal "RC4") "Seed stuff") 'rbi) n)

for n>1 yields a generator of integers uniformly distributed in [0, n).

(((fileVal "RC4") "Seed stuff") 'U)

yields a generator of floats (‘inexacts’) uniformly between 0 and 1.

More info

RC4d

((fileVal "RC4d") seed n) produces a value like ((fileVal "RC4") seed) except that the first n bytes have been produced and discarded. Some literature refers to this variation as “RC4 drop n”.

crypto

Nascent numeric crypto

Coin

((fileVal "Coin") seed) generates a fair coin—a stream of random bools.
(let ((c ((fileVal "Coin") "Jilt"))) (list (c) (c) (c))) => (#f #f #t).

bCoin

((fileVal "bCoin") seed) generates a coin with adjustable probability.
((fileVal "bCoin") "Thule") returns a coin which is a function of one argument which is between 0 and 1. If c is such a coin then the probability of (c x) is x.

AGEC and AGECp

Abelian Group from Elliptic Curve; See this.

RND

Generator of sequences of random normal deviates.

(let ((sg ((fileVal "RND") "frSeed"))) (let r ((n 10000) (m 0) (s 0))
  (if (zero? n) (cons m s) (let ((w (sg))) (r (- n 1) (+ m w) (+ s (* w w)))))))

yields (41.62913630233171 . 10215.783961421654).

rr

Random rational generator

(let ((g ((fileVal "rr") "Seed"))) (list (g) (g)))

yields (-37/113 125/23).

binomial

Binomial coefficients: ((fileVal "binomial") p q) = C(p, q).

egcd

Extended Euclidean Algorithm.
((fileVal "egcd") a b) yields (x . y) such that ax+by = (gcd a b)
((fileVal "egcd") 100 144) => (13 . -9)
gcd(100, 144) = 4, 1300 − 1296 = 4

Factorial

((fileVal "Factorial") n) yields n! for n > −1. It works for integral and half integral values.
((fileVal "Factorial") -1/2) => (−1/2)! = 1.7724538509055159 = √π.

expt

((fileVal "expt") op one inv) returns a function pow such that (pow k n) returns kⁿ where n is an integer, k is in some algebra, op is an associative operator in that algebra, and the following rules hold:

(pow e 0) = one
(pow e 1) = e
(pow e (+ m n)) = (op (pow e m) (pow e n))
(eq? (op e (inv e)) one)

The provided inv function will be invoked only for negative powers. The time is the product of an op time and the log of n.

gamma

Definition: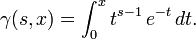

Calculation: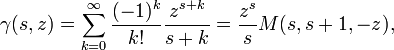

The incomplete Gamma function
((fileVal "gamma") s z) => γ(s, z). For constant s and large values of z γ(s, z) is asymptotic to some constant. Power series don’t do this well. This Algol68 code can run in multiple precision so as to extend the range.

Chi2

The χ² distribution, both density:

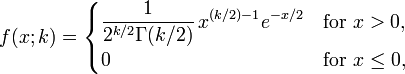
(((fileVal "Chi2") 'f) x k) = f(x; k)
and cumulative:

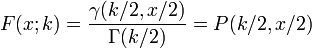
(((fileVal "Chi2") 'F) x k) = F(x; k)
A meagre corroboration

int

((fileVal "int") x0 x1 k f) yields a crude integral of f using k equally spaced points from x0 to x1.

pias

To search an arithmetic sequence for the first prime. Candidates are tested with the Miller−Rabin primality test.

((fileVal "pias") a b)

returns the first prime among a + nb for n = 0, 1, 2, ... . The value ("Always divisible by" n) is returned instead if a and b are both divisible by n and n > 1. If a and b are relatively prime there are such primes. There is extraneous printed output during the computation consisting of a comma for each candidate which is excluded for being divisible by a prime less than 18, and a construct such as (123 #f) when the Miller−Rabin test finds the candidate to be composite for n = 123. Running this program for largish numbers suggests that the probability of false positives is very much less than 1/2 which is the proven upper bound on the probability. Indeed I have seen no false positives in a few hundred cases.

((fileVal "pias") (expt 10 100) -1) indicates that 10¹⁰⁰ − 797 is the largest prime less than 10¹⁰⁰. (10¹⁰⁰⁰−1769 is prime too.) more info.

piasd

like pias above but if result is p then both p and 2p+1 are prime. (p is a Sophie Germain prime.)

mod-exp

((fileVal "mod-exp") p q m) yields p^q modulo m. p, q and m are integers: q ≥ 0 and m ≥ 2.

Miller-Rabin

The Miller−Rabin primality test: If p is prime and 1 < a < p−1 then (((fileVal "Miller-Rabin") 'base) a p) is true. If p is composite then it is false for almost all such a’s. Cumulative count of false positives less than 5ⁿ for the composite 2²⁵+1: (3 5 7 10 12 14 19 25 … )

((((fileVal "Miller-Rabin") 'multi) n) p) chooses n random probes to test p for primality. #t is returned if each Miller-Rabine probe reports that p is prime. (((fileVal "Miller-Rabin") 'multi) n) denotes the object that is mutable by virtue of carrying the PRNG to choose the random probes.

try or try1

Conventional try-catch function.

((fileVal "try") (lambda (e) (write "working") 'w)
     (lambda (t) (write (list "exception" t)) 'e))
     ; => "working"w
((fileVal "try") (lambda (e) (write "attempting") (e "peculiar") (write "never gets here!"))
     (lambda (t) (write (list "exception" t)) 'e))
     ; => "attempting"("exception" "peculiar")e

try1 guards agains multiple invocation of e. See More info.

gr

Changes a function of zots into a function of lists of zots, returning a list of results. If gr = (fileVal "gr") then ((gr odd?) '(1 2 3 4 5)) yields (#t #f #t #f #t) and ((gr +) '(2 3 4 5) '(9 7 5 3)) yields (11 10 9 8).

transpose

(fileVal "transpose") transposes a matrix expressed as a non-empty list of equal length lists.

transpose0

((fileVal "transpose0") 0 zero?) is a function that transposes an infinite list of infinite lists where all but a finite number of terms are terminal zeros and omitted. Trailing all zero rows are also omitted. Adding a 0 to the end of a matrix row or adding an empty row to the end of a matrix results in a Scheme value denotation the same infinite matrix. More info

sort

Unstable sort;

((fileVal "sort") '(5 3 4 882 3 5 44 3 9 -7) <) => (-7 3 3 3 4 5 5 9 44 882)

Set

A suite of set functions. Transcribed from a source with a GNU license. The suite is parameterized by a total ordering function for set elements. If sy is a symbol from the list of values listed here, then (((fileVal "Set") comp) 'sy) yields the value described on the same page. (comp a b) must return a negative number, 0, or a positive number depending on whether a<b, a=b or a>b respectively. ((fileVal "Set") -) returns a map from symbols to set tools, in this case sets of numbers. If m is such a map then (m 'union) returns the set-union operator. See this for more detail.

HSet

has the same specifications as module ‘Set’ above but uses module ‘Seal’ q.v. to impose abstraction. ((fileVal "HSet") 'Set?) yields a predicate for being a set of this variety.

Whereas (let* ((s ((fileVal "HSet") -))) ((s 'choose) ((s 'singleton) 42))) yields 42, (let* ((r (fileVal "HSet")) (s1 (r -)) (s2 (r -))) ((s1 'choose) ((s2 'singleton) 42))) fails ignominiously. These both yield 42 for module "Set".

“(fileVal "TestSet")” performs a test suite on both Set and HSet.

Farey

Farey Sequence: ((fileVal "Farey") n) => F_n.

ContFrac

Continued Fractions: If x is (fileVal "ContFrac") and n is a positive integer and y is a positive number then ((car x) y n) produces a list of up to n terms of the continued fraction for y. The list may be shorter if x is an exact rational. If z>0 and n is large enough then ((cdr x) ((car x) z n)) should yield z within floating point precision.

stream

Routines to convert between streams and lists.

(ylppa (fileVal "stream") (lambda (sm si SG->lst lst->SG fs Cart string->SG)
; Scope of stream functions
(SG->lst (sm (si 6) -)) ; => (0 -1 -2 -3 -4 -5)
))

more detail

BiasBin

Conversion to and from biased radix 2 representation. If 0<b<1, 0<x<1 and n is a non-negative integer then
(let ((p ((fileVal "BiasBin") b))) (= ((cdr p) ((car p) x n)) x)) yields true, especially if b and x are exact. more info

Matrix

Determinants and matrix functions over arbitrary fields. A matrix is a list of vectors and vector is a list of field elements.

Arguments to (fileVal "Matrix")

• Random scalar generator
• the zero element for the field
• a predicate that tests its field argument for being zero
• the multiplicative identity of the field
• the operator that adds two field arguments
• the unary additive inverse function
• the operator that multiplies two field arguments
• the multiplicative inverse function

Yields the list:

• Random n×n Matrix Generator (rmg n)
• Matrix multiplication
• Matrix inversion (2nd arg is continuation for singular matrix)
• Inner product of two vectors
• Transpose
• Determinant
• Identity test (Is this the identity matrix?)
• Binary vector equality test
• Binary matrix equality test

(rmg k) returns a random k by k matrix. They may deployed:

(ylppa ((fileVal "Matrix") '() 0 zero? 1 + - * /)
(lambda (rm matm matinv ip tr det i? v= m=)
; Scope of matrix functions over Scheme numbers
(det '((1 3 2)(4 0.6 2)(3 8 4)))
)) ; => 16.8

If the ‘Matrix Generator’ is not used then the ‘Random scalar generator’ is not used. Note that we do not supply a good random scalar generator since we do not need a random matrix generator.

The 2nd argument to the produced inversion routine is a continuation which is invoked for a singular matrix, passing a vector which, when padded with sufficient zeros, yields x such that Mx = 0. See this for critical application of this value.

(ylppa ((fileVal "Matrix") '() 0 zero? 1 + - * /)
(lambda (rm matm matinv ip tr det i? v= m=)
  ((fileVal "Try") (lambda (e) (matinv '((2 3 5) (6 9 4) (8 12 9)) e))
    (lambda (v) (write v)))))

yields (-3/2 1) since the first two columns are dependent.

The code inverts matrices of quaternions; see quatApp below. Thus it probably handles division rings. It even inverts matrices in associative algebras with dense inverses such as Clifford Matrices.
More info

MatInverse

A concrete matrix invert built from above.

((fileVal "MatInverse") '((2 4 5)(3 2 5)(5 7 4)))

yields ((-27/53 19/53 10/53) (13/53 -17/53 5/53) (11/53 6/53 -8/53)). Any Scheme numbers may be used including, rational, complex and floating point.

GenDiag

((fileVal "GenDiag") n d b) returns a list of n lists each with n elements. The jth elements of the jth list is d and the other elements are b. ((fileVal "GenDiag") n 1 0) returns the n by n identity matrix.

HilbertMat & HilbertM

((fileVal "HilbertMat") n) produces the infamous nth Hilbert matrix and ((fileVal "HilbertM") n) inverts that and reports its determinant and inverse.

diag

((fileVal "diag") num-list) yields a diagonal matrix with elements of num-list down the diagonal.

ranoth

((fileVal "ranoth") "ran seed" n) yields a generator of random orthogonal n by n real matrices, i.e. matrices from O(n). The distribution is invariant over O(n). Adapted from this. Notes on testing.

gRREF

Reduced Row Echelon Form of matrix parameterized by field.

(let ((R ((fileVal "gRREF") zero? 0 1 / * - C)))
   ((R 'rref) m) ; Reduced Row Echelon Form of matrix m.
   ((R 'rank) m) ; rank of m
   ((R 'minspan) m) ; spanning subset of m
)

Arguments - and * are binary; / is unary. Argument C is for ‘canonical’. If C is true then the resulting transformation omits trailing zero vectors and this modification makes the matrix canonical with respect to which subspace its vectors span. The classical definition of RREF requires as many rows in the output as in the input. The returned RREF function returns the classical answer if C is false (#f). more info

Intersect

Compute intersection of subspaces of vector space where subspaces are denoted by a lists of spanning vectors. ((fileVal "Intersect") a b) yields the intersection. See demos at end of source and here. Detailed info

gIntersect

Specification. Compute intersection of subspaces of vector space over field where subspaces are identified by a list of spanning vectors. See demos at end of source and here.

If A is the matrix of the coefficients of a set of homogeneous linear equations then ((((fileVal "gIntersect") 0 zero? 1 + - * /) 'oss) A 0) yields a minimal list of solutions that span the space of all solutions. more info

testInter

Code to test gIntersect above. More info.

PGc

Projective Geometry: Specs

PGLat

Verifying lattice properties of subspaces (fileVal "PGLat") => (#t #t)

Desargues

Corroborating Desargues’ theorem. comments

Polynomial tools

Several tools where given a ring R, a polynomial ring K[R] is returned and given a field a gcd is provided. A transcendental field extension is also provided. (fileVal "transpose0") will be useful in some related applications.
Some terminology and fundamental notions.

finFieldMat

((fileVal "finFieldMat") p q n) yields some tools for n by n matrices whose elements are from GF(p^q). The yield is (random mp inv ip tr deter it? v= m=). Returned values are those of Matrix.

finFieldMatTest

((fileVal "finFieldMatTest") p q n) runs a test of the above finite field n by n matrix logic from GF(p^q).

Jacobi

((fileVal "Jacobi") a n) is the Jacobi symbol sometimes written .

DivisionAlgebra

(fileVal "DivisionAlgebra") automates the Cayley-Diskson construction of the Division Algebras. (fileVal "DivisionAlgebra") yields the list (G reals e) where (G(G reals)) yields the Quaternions, for example and (e 4 j) yields e_j which is the jth basis element of the level four algebra. More info

k4ZerDiv

Zero Divisors in Sedenions

divAlgSurvey

(fileVal "divAlgSurvey") builds the first five Cayley-Diskson algebras and reports their algebraic properites. More info

quaternion

(fileVal "quaternion") yields a list of quaternion tools:
(random quaternion generator, zero, zero predicate, one, addition, negation, multiplication, inverse). Here is an alternate ab-initio construction of the quaternions.

quatApp

(fileVal "quatApp") builds matrices of quaternions and successfully inverts them with Matrix!

GFp

For a prime p, ((fileVal "GFp") p) yields a list of the four operations over GF(p): +, −, *, /. The ops − and / are unary, the operands are non negative integers less than p.

GFsqrt

is a modular square root routine. If p is prime and 0≤n≤p then (((fileVal "GFsqrt") p) (* r r)) yields r or p−r. If x is not a quadratic residue modulo p then it returns 'none. This and this address the other finite fields.

finiteField

Code to perform arithmetic over any finite field. This module exports tools of interest to builders of alternate representations. Detailed specs are here. Most users want GFpq below.

GFpq

((fileVal "GFpq") p q st) returns a tool list

• sample generator, (() → F)
• zero, (F)
• zero predicate, (F → bool)
• one, (F)
• add, (F×F → F)
• negate, (F → F)
• times, (F×F → F)
• invert, (F → F)

such as needed for input to the Matrix module. The finite field is GF(p^q) and st is a non-empty string which only seeds the random ‘sample generator’. The following illustrates matrices from Finite fields:

(ylppa (ylppa ((fileVal "GFpq") 17 4 "p") (fileVal "Matrix"))
  (lambda (rmg mm inv ip tr det i? v= m=)
  (let ((inv (lambda (q) ((fileVal "try") (lambda (w) (inv q w))(lambda (e) "e")))))
  (let* ((m (rmg 4))(mi (inv m))) (list m mi (inv mi) (i? (mm m mi)))))))
=> (…, …, …, #t)

See this if you need the irreducible polynomial.

rip

((fileVal "rip") p q) searches randomly for irreducible polynomials of degree q over GF(p). Perhaps there are no 5th order irreducible binomials over GF(6700417) and searching lexicographically is thus frustrating. They are abundant further on.
((fileVal "rip") 6700417 5) yields (8 . #6(5538386 4064128 2588321 4310749 3668254 1)). It took 8 trials to find this irreducible polynomial.

ffqr

((fileVal "ffqr") p q) counts quadratic residues in finite field GF(p^q). See theorem.

LagCoef

((fileVal "LagCoef") '() 0 zero? 1 + - * /) provides a function LC over the field of Scheme numbers that produces Lagrange coefficients. Like "Matrix", "LagCoef" can take other field tools as illustrated in the last demo.

Clifford0

Simplest Clifford algebra. (fileVal "Clifford0") => (functor reals) where (functor Cⁿ) generates Cⁿ⁺¹ and reals is the reals. More info More info

Clifford1

Fuller Clifford algebra. More info

CliffTst1

Simple corroboration of above. (fileVal "CliffTst1") => #t. More info

Clifford2

Fuller Clifford algebra with pretty good division. More info

CliffTst2

Simple corroboration of above. (fileVal "CliffTst2") => #t. More info

IndCliff

Clifford studied algebras based on negative definite quadratic forms. This package generates ‘Clifford algebras’ based on indefinite forms. ((fileVal "IndCliff") (list + - - -)) generates a pseudo Clifford algebra where γ₀² = 1 instead of −1. See test code at end of file for the returned values. more info

IndCliffTst

Demonstration of isometry with explanation.

CliffordTurn

Demo of how Clifford algebras bear on isometry. ((fileVal "CliffordTurn") (list - - - +)) explores Minkowsky’s space.

CliffMat

(fileVal "CliffMat") Generates a 3×3 matrix of Clifford numbers (Cl(3)) using small rationals. It inverts the matrix using the ‘almost everywhere inverse’. It checks that the inverse times the original is the identity.

CliffMat2

(fileVal "CliffMat2") Generates a 5×5 matrix of Clifford numbers (Cl(4)) using random normal deviates as constituent floating point reals. It inverts the matrix using the ‘almost everywhere inverse’. It checks that the inverse times the original is the identity within a tolerance of 2⁻⁴⁸.

Shannon

Shannon’s information formula for a symbol chosen from a given probability distribution. Argument is list of probabilities which should sum to 1.

SRFI-60

A standard but not required extension to Scheme that exposes the bits in integers. (fileVal "SRFI-60") returns a list of the 19 functions specified in the SRFI-60. If xxx is a body of code using the preferred names in the SRFI then (apply (lambda (logand logior logxor lognot bitwise-if logtest logcount integer-length log2-binary-factors logbit? copy-bit bit-field copy-bit-field ash rotate-bit-field reverse-bit-field integer->list list->integer booleans->integer) xxx) (fileVal "SRFI-60")) performs xxx with those 19 bindings. This exploits the partial implementation of MzScheme.

once

Protect against attack by continuation. (((fileVal "once") p) a) performs as (apply p a) returning at most once despite attempts in p to use the continuation mechanism to return twice.

EPR

A generator of Einstein Podolski Rosen entangled photon pairs. More info
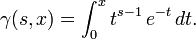
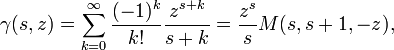
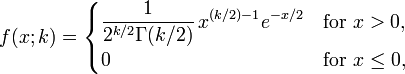
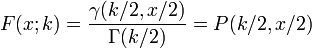